1. 动态数组
它的基本思路是使用如malloc/free等内存分配函数得到一个指向一大块内存的指针,以数组的方式引用这块内存或者直接调用动态数组的接口,根据其内部的实现机制自行扩充空间,动态增长并能快速地清空数组,对数据进行排序和遍历。
它的数据结构定义如下:
typedefstruct {void *data;int capacity;int index;int type_size;int (*comp)(constvoid *,constvoid *); } array_t;
- data表示: 指向一块连续内存的指针;type_size: 元素类型的大小(动态执行时才能确定类型)
- capacity: 动态数组的容量大小,最大可用空间 ; index: 动态数组的实际大小
int (*comp)(const void *,const void *): 元素的大小比较函数,comp为函数指针
2. 链表
链式存储是最通用的存储方式之一,它不要求逻辑上的相邻的元素物理位置上相邻,仅通过链接关系建立起来。链表解决了顺序表需要大量的连续存储空间的缺点,但链表附加指针域,也带来了浪费存储空间的缺点。
它有多种多样的结构,如:
- 只含一个指针域的单链表、
- 含指向前后结点两个指针域的双链表
- 首尾相连的循环链表(单向或双向)
- 块状链表(chunklist)
- 跳跃链表
A 单链表
对于链表这种结构,有时候第一个节点可能会被删除或者在之前添加一个节点,使得头指针指向的节点有所改变。消除这些特殊情况的方法是在链表的第一个节点前存储一个永远不会被删除的虚拟节点,我们称之为头节点,头结点的数据域可以不设任何信息也可以记录表长等信息。
头结点的指针域指向的是真正的第一个节点,从实现中可以看到它极大地简化了插入和删除操作,也避免了在C中使用二级指针跟踪记录头指针的变化。为了比较使用头结点和不使用头结点的区别,实现的单链表采取不使用头结点的方法,双向循环链表使用头结点,加深对链表操作的理解。
B 块状链表
对于块状链表来说,它本身是一个链表,但链表存储的每个结点是一个数组。如果数组有序,结合链表的顺序遍历(链表是非随机访问的)和有序数组的折半查找可以加快数据的查找速度,在某些情况下对于特殊的插入或删除,它的时间复杂度O(n^(1/2))
并且相对于普通链表来说节省内存,因为它不用保存指向每一个数据结点的指针。
C 跳表
对于跳跃链表,它是一种随机化的数据结构,在有序的链表上增加附加的前进链接,增加是以随机化的方式进行的,所以列表的查找可以快速跳过部分列表而得名。在实际中它的工作性能很好 ,这种随机化平衡方案比在平衡二叉树中用到的确定性平衡方案更容易实现,并且在并行计算中也很有用。
2.1 单链表
链表中节点类型描述如下:
typedefstruct list_node {void *item;struct list_node *next; } list_node_t;
对应地,单链表的数据结构定义如下:
typedefstruct slist { list_node_t*head;int n;int (*comp)(constvoid *,constvoid *); } slist_t;
这里的head指针既可以定义为头指针,指向链表的第一个节点,即空表初始化为NULL;它也可以定义为虚拟的头结点,分配一个节点的内存,它的指针域指向链表的实际结点。这里先使用不带头结点的方法实现单链表的操作
2.1.1 单链表的插入和删除操作
A 单链表的删除操作
如果在链表尾部插入,要考虑如果链表为空的话尾部的插入同样需要更新头指针,它的实现如下:
/*在单链表尾部添加元素*/void slist_push_back(slist_t *l,void *item) {/*构造新结点*/ list_node_t*node=new_list_node(item);if(l->head){ list_node_t*cur=l->head;while(cur->next){ cur=cur->next; } cur->next=node; }else { l->head=node; } l->n++; }
在链表头部添加元素比较简单,实现如下:
/*在单链表头部添加元素*/void slist_push_front(slist_t *l,void *item) { list_node_t*node=new_list_node(item); node->next=l->head; l->head=node;//无需区分头指针是否为空,情形一样 l->n++; }
因而如果插入的节点是链表的第i个位置,就需要讨论插入的情形: 头部插入、尾部插入、中间插入,这里不给出具体实现。
B 单链表的删除操作
如果在链表尾部删除元素,分两种情形删除: 链表只有一个节点时、链表不止一个结点。对于含有多个结点的链表,需要维持一个prev指针记录尾部元素的上一个结点再进行删除操作。实现如下:
/*在单链表尾部删除元素,若存在,返回被删除的元素键值,否则返回NULL*/void *slist_pop_back(slist_t *l) { list_node_t*cur,*prev;if(l->head){void *res_item;if(l->head->next){//不止一个结点 prev=l->head; cur=l->head->next;while(cur->next){ prev=cur; cur=cur->next; } prev->next=NULL; }else {//只有一个节点 cur=l->head; l->head=NULL; } res_item=cur->item;free(cur); l->n--;return res_item; }return NULL; }
在链表头部删除元素比较简单,实现如下:
/*在单链表头部删除元素,若存在返回被删除的元素键值,否则返回NULL*/void *slist_pop_front(slist_t *l) { list_node_t*cur;if(l->head){ cur=l->head; l->head=l->head->next;void *res_item=cur->item;free(cur); l->n--;return res_item; }return NULL; }
另外一个删除操作是:删除单链表中第一个含item值的节点,它的实现和尾部删除类似,同样需要讨论删除情形。具体实现如下:
/*在单链表中找到第一个含item值的节点并删除此节点*/void *slist_delete(slist_t *l,void *item) { list_node_t*cur,*prev;int (*comp)(constvoid *,constvoid *); comp=l->comp; prev=NULL; cur=l->head;while(cur){int cmp_res=comp(item,cur->item);if(cmp_res==0){break; }else { prev=cur; cur=cur->next; } }if(cur==NULL){//该键值不存在或者链表为空return NULL; }else {if(prev==NULL)//删除的是第一个节点return slist_pop_front(l);else { prev->next=cur->next;void *res_item=cur->item;free(cur); l->n--;return res_item; } } }
2.2 双向循环链表
双向循环链表中的节点类型描述如下:
typedefstruct dlist_node {void *item;struct dlist_node *prev;struct dlist_node *next; } dlist_node_t;
对应地,双向循环链表的数据结构定义如下:
typedefstruct { dlist_node_t*head;int n;int (*comp)(constvoid *,constvoid *); } dlist_t;/*创建一个元素节点,让头尾都指向自己并设元素值*/static inline dlist_node_t *new_dlist_node(void *item){ dlist_node_t*node=malloc(sizeof(dlist_node_t)); node->prev=node->next=node; node->item=item;return node; }
在双向循环链表的实现中,使用的head指针为虚拟的头结点,实现方式如下:
/** * 为双向循环链表分配内存,两种思路: * 不带头节点,通过判断l->head是否为NULL来删除链表 * 带头节点,只需判断cur=l->head->next与l->head的是否相等(l->head==l->head->next才为链表空) * 单链表实现中使用了不带头节点的办法(注释说明的头结点只是链表头指针),双向链表我使用带头节点的思路 * 也是为了比较这两种方法哪个适合简化插入和删除操作*/ dlist_t*dlist_alloc(int (*comp)(constvoid *,constvoid *)){ dlist_t*l=malloc(sizeof(dlist_t)); l->head=new_dlist_node(NULL); l->n=0; l->comp=comp;return l; }
从后面的实现可以看出它极大简化了链表的插入和删除操作。
2.2.1 循环双链表的插入和删除操作
由于使用的是带头结点的循环双链表,它判空的标志是l->head==l->head->next,一定要明确,这是判断遍历是否结束的标记。
A 查找循环双链表中第i个位置的结点
为了简化插入和删除操作,假设第0个位置的节点为虚拟的头结点(很关键),使得插入和删除完全统一起来实现如下:
/*查找双链表第pos个位置的节点,pos从0开始*/ dlist_node_t*dlist_find_pos(dlist_t *l,int pos){if(pos<0 ||pos>l->n){ printf("Invalid position to find!\n");return NULL; }if(pos==0){return l->head;//头部插入,关键点,使得所有插入统一化了 } dlist_node_t*cur=l->head->next;int j=1;//计数从1开始表示while(cur!=l->head){//链表为空的标志if(j==pos){break; } cur=cur->next; j++; }return cur; }
B 插入操作
在双向循环链表某位置添加元素,可插入的pos范围:0-l->n
- pos为0时表示头部插入
- pos为
l->n时表示尾部插入
关于双链表的插入方式,tmp指针要插入在cur指针后,要么两节点前驱后后继同时链上,要么先链一个方向再链另外一个方向,方式不同效果相同。实现的技巧就在于基于位置查找的函数在pos=0时返回头指针,使得插入任何位置都使用统一的代码。 实现如下:
void dlist_insert(dlist_t *l,void *item,int pos){if(pos<0|| pos>l->n){ printf("Invalid position");return; } dlist_node_t*cur=dlist_find_pos(l,pos);//定位到pos位置的节点 dlist_node_t *tmp=new_dlist_node(item); ;//插入到pos位置的新节点 tmp->next=cur->next; cur->next->prev=tmp; tmp->prev=cur; cur->next=tmp; l->n++; }
C 删除操作
删除操作的思路是要先找到删除位置的前驱结点,当删除的是第一个结点时由于位置查找的函数同样也可以返回第0个位置的结点指针(返回头结点),同样使得删除操作都可以使用一致的代码。实现如下:
/*在双向循环链表中删除pos位置节点并输出当前值,pos从1到l->n*/void *dlist_delete(dlist_t *l,int pos){if(pos<1|| pos>l->n){ printf("Invalid position");return NULL; } dlist_node_t*cur=dlist_find_pos(l,pos-1);//找到删除位置的前驱节点 dlist_node_t *tmp=cur->next;//被删除位置的节点 cur->next=tmp->next; tmp->next->prev=cur;void *res_item=tmp->item;free(tmp); l->n--;return res_item; }
2.3 跳跃表skiplist
在字典的实现中,通常使用平衡二叉树会得到较好的性能保证,例如AVL tree、Red-Black tree、Self-adjusting trees。对于除伸展树外(单个操作是O(n)的时间复杂度)的一些平衡树,它们的插入、删除等操作一般有对数级别的时间复杂度。但它们的缺点是需要维护二叉树平衡的信息,在实现上有一定的难度,显然数据结构的随机化比维护平衡信息更容易实现。
定义跳跃表节点和跳跃表的数据结构如下:
typedefstruct skiplist_node {void *item;struct skiplist_node *forward[1]; } skiplist_node_t; typedefstruct { skiplist_node_t*head; skiplist_node_t**update;double prob;int max_level;int level;int (*comp)(constvoid *,constvoid *);int n; } skiplist_t;
为了灵活性,在跳表结点的结构定义中,把结点指向某个含有键值对的表项而非整数键
item: 表示结点的数据项forward: 长度为1的柔性数组,切记节点的大小包括一个数组元素(与长度为0的数组大小不想同)- 柔性数组: 表明每个节点对应的
forward数组是变长的
在跳表的数据结构定义中:
head: 为了简化插入和删除操作,定义一个虚拟头结点,它含有最大层次+1个forward前向指针update数组: 用于在插入、删除、查找操作中更新每个层级被查找节点的前驱指针。它在跳表初始化时就被创建,防止了每次在进行插入等操作时需要分配和释放该数组的内存prob: 某节点被创建时出现在某层次的概率。 它的概率分布类似于丢硬币实验,连续i次出现同种情形(如正面)对应i的次数的分布。很显然它满足参数为p的几何分布,期望值为1/plevel: 跳表当前的最大层次comp: 比较跳表中表项大小的函数n: 当前存储在跳表中的元素个数
建议我们理想中开始查找的层次为L(N)=log(N)/log(1/p)。例如p=0.5时,处理至多含有2^16个数据的跳表最大的层次是16,即定义中的max_level。
2.3.1 跳表的插入、删除、查找操作
A 跳表的初始化和节点层次的随机化生成
在初始化跳表时需要明确几点:
- 跳表的最大层次的计算公式:
int max_level= -log(N)/log(prob);。例如prob=0.5,8个节点的跳表它应该有0,1,2,3层 - 链表头结点有
max_level+1个前向指针,从0开始初始化(头结点本身含有1个level 0级别的前向指针,再加上借助柔性数组扩展的max_level个前向指针) - 对于某层次i的前向指针为NULL表示该层级上的虚拟链表为空
- 为防止每次插入或删除操作时要重复分配update数组预先初始化
它实现如下:
skiplist_t *skiplist_alloc(int capacity,double prob,int (*comp)(constvoid *,constvoid *)){ skiplist_t*l=malloc(sizeof(skiplist_t)); l->prob=prob; l->comp=comp;/*注gcc的数学函数定义在libm.so文件例,需链接上数学库,编译时添加 -lm选项*/int max_level= -log(capacity)/log(prob);//这个指的是最高的层级max_level,例如8个节点的话有0,1,2,3层 l->max_level=max_level;//例如max_level为16 l->level=0; l->head=new_skiplist_node(max_level,NULL);/*更新头结点的forward数组为NULL*/for(int i=0;i<=max_level;i++){ l->head->forward[i]=NULL; }/*为防止每次插入或删除操作时要重复分配update数组*/ l->update=malloc((max_level+1)*sizeof(skiplist_node_t *)); l->n=0;return l; }
节点层次的随机化生成,要点有两个:
- 链表的层次为i,表示若随机生成的level大于i则i层次以上的前向指针均指向为NULL
- 生成的level值范围是0-max_level,但这种随机数的生成效果并不是最佳的,它也可能出现某些层次以上的元素完全相同
它的实现如下:
int rand_level(double prob,int max_level){int level;int rand_mark=prob*RAND_MAX;for(level=0; rand()) ;return level; }
B 跳表的插入和删除操作
插入和删除操作的核心在于简单的搜索和拆分(要么插入要么删除)。通过查找键在每个层次所属的位置,记录在一个update数组中。update[i]表示的是插入和删除位置的最右左边位置(个人称之为插入或删除位置的前驱指针)。如下图:
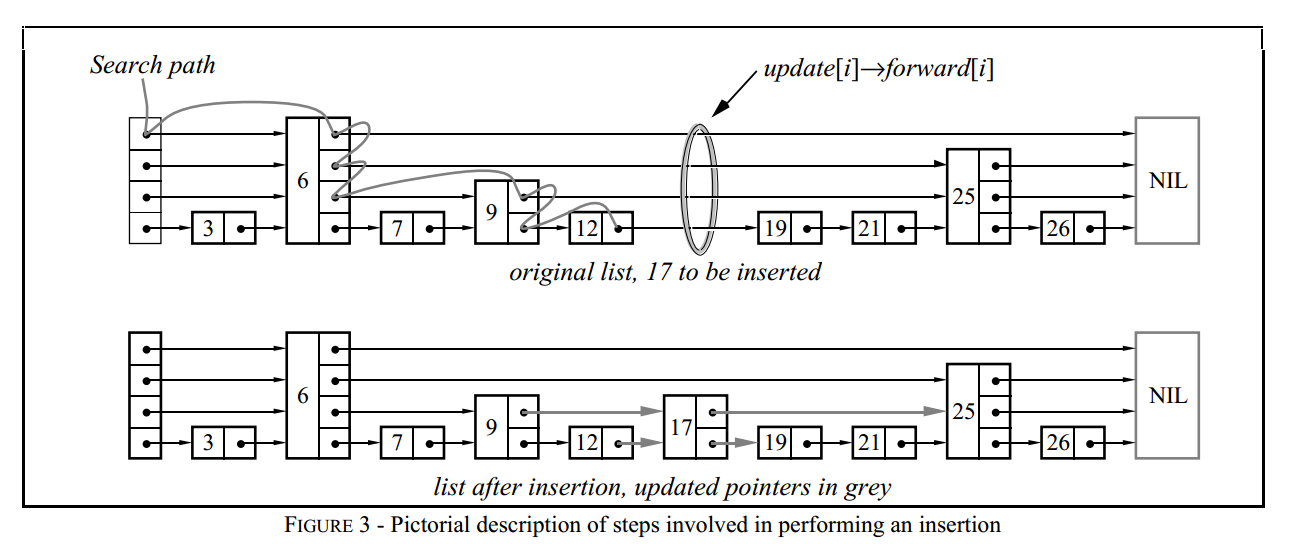
插入操作的要点如下:
- 找到待插入的位置(在当前元素的前向指针的键与元素的键相等或者大于的适合退出),再更新每个层次的update数组
- 随机生成新节点的level
- 调整指向,插入新节点
删除操作的要点如下:
- 找到要调整位置的前驱指针
- 自底层向高层进行节点的删除并释放该节点内存
- 更新跳表的level(由于某些节点的删除可能会使部分高层次的前向指针为NULL)
查找操作就比较简单,它是插入或删除操作的第一个步骤。三个操作的实现如下:
void *skiplist_insert(skiplist_t *l,void *item){ skiplist_node_t*cur=l->head; skiplist_node_t**update=l->update;int (*comp)(constvoid *,constvoid *); comp=l->comp;int i;/*查找键所属的位置*/for(i=l->level;i>=0;i--){while(cur->forward[i]!=NULL &&comp(cur->forward[i]->item,item)<0) cur=cur->forward[i];//在当前层次遍历直至前向指针为NULL或者对应的前向指针的元素大于或等于item update[i]=cur;//更新插入位置的前驱指针 } cur=cur->forward[0];if(cur!=NULL&&comp(cur->item,item)==0)return cur->item;//键值已存在,直接返回原来的节点int level=rand_level(l->prob,l->max_level);//最大的level控制在max_levelif(level> l->level){//如果新生成的层数比跳表层数大,更新下标大于i的update数组指向为头结点for(i=l->level+1;i<=level;i++){//持续到当前生成的level上 update[i]=l->head; } l->level=level;//更新自己的层级数 } skiplist_node_t*tmp=new_skiplist_node(level,item);/** * 调整前向指针的指向,插入新结点 * 问题就出现在这里,注意如果生成的level级别较低,只需要在从0..level的级别进行插入,切记不能使用l->level * l->level和level是有不同的,除非level大于当前跳表的level时*/for(i=0;i<=level;i++){ tmp->forward[i]=update[i]->forward[i]; update[i]->forward[i]=tmp; } l->n++;return NULL; }/*在跳表中进行查找,找到返回当前元素的item否则返回NULL*/void *skiplist_find(skiplist_t *l,void *key_item){/*查找是否含有当前的元素*/ skiplist_node_t*cur=l->head; skiplist_node_t**update=l->update;int (*comp)(constvoid *,constvoid *); comp=l->comp;int i,res;for(i=l->level;i>=0;i--){while(cur->forward[i]!=NULL &&((res=comp(cur->forward[i]->item,key_item))<0)) cur=cur->forward[i];//在当前层次遍历直至前向指针为NULL或者对应的前向指针的元素大于或等于item update[i]=cur;//更新插入位置的前驱指针 } cur=cur->forward[0];if(cur!=NULL&&comp(cur->item,key_item)==0){return cur->item; }return NULL; }void *skiplist_delete(skiplist_t *l,void *item){ skiplist_node_t*cur=l->head; skiplist_node_t**update=l->update;int (*comp)(constvoid *,constvoid *); comp=l->comp;int i;int level=l->level;for(i=level;i>=0;i--){while(cur->forward[i]&&comp(cur->forward[i]->item,item)<0) cur=cur->forward[i]; update[i]=cur; } cur=cur->forward[0];if(cur==NULL||comp(cur->item,item)!=0)return NULL;//键值不存在for(i=0;i<=level;i++){if(update[i]->forward[i]!=cur)break;//若低层次的前向指针不包括cur,则高层次就不可能存在(高层次的链表是低层次的子链表) update[i]->forward[i]=cur->forward[i]; }void *ret_item=cur->item; l->n--;free(cur);while(l->level>0 &&l->head->forward[l->level]==NULL) l->level--;return ret_item; }
2.3.2 总结
尽管跳表在wort-case时会生成一个糟糕的不平衡结构,没法和平衡树一样保证较好的最坏或均摊的性能,但发生这个情形的概率很小。并且它在实际工作中效果很好,对于很多应用来说,随机化的平衡方法-跳跃链表相比平衡树树而言,它是一种更自然的表示,并且算法更为简单,实现起来更为容易,比平衡树具有更好的常数优化性能。
下面是一些使用跳表的应用和框架列表,可见相比平衡树,跳跃表还是有很多实际应用的
- Lucene: 使用跳表在对数时间内search delta-encoded posting lists
- Redis: 基于跳表实现它的有序集合
- nessDB: a very fast key-value embedded Database Storage Engine (Using log-structured-merge (LSM) trees), uses skip lists for its memtable
- skipdb: 一个开源的基于跳跃表实现的可移植的支持ACID事务操作的Berkeley DB分割的数据库
- ConcurrentSkipListSet and ConcurrentSkipListMap in the Java 1.6 API.
- leveldb: a fast key-value storage library written at Google that provides an ordered mapping from string keys to string values
- Skip lists are used for efficient statistical computations of running medians (also known as moving medians)。
另外跳跃表也可应用在分布式应用中,用来实现高扩展性的并发优先级队列和并发词典(使用少量的锁或者基于无锁),所以学习基于随机化技术的跳跃表是很有必要的。