Unity 贝塞尔曲线之美

 最近项目中用到了贝塞尔曲线，学习完成后记录一下自己的学习结果吧。

一阶贝塞尔曲线

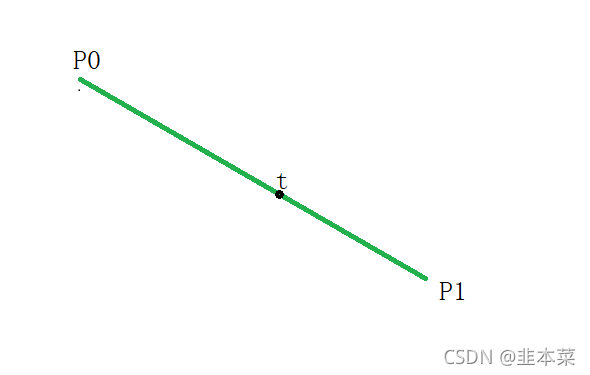
 一阶贝塞尔曲线就是一条线，我们很容易根据 t 求出 t 点的位置。

P(t)=P0+(P1-P0)*t =(1-t)*P0+tP1  ；   t[ 0,1] ,且其等同于线性插值。

二阶贝塞尔曲线

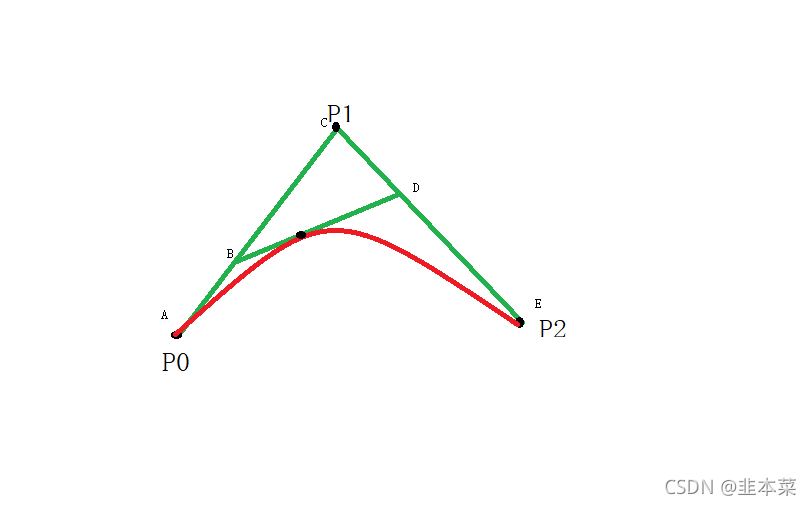
取平面内三个不共线的点，AB:AC=CD:CE,这个时候BD又是一条直线，可以按照一阶的贝塞尔方程来进行线性插值了。

P(B)=(1-t)*P0+tP1 ;

P(D)=(1-t)P1+tP2  ;

P(t)=(1-t)*P(B)+tP(D) 

=(1-t)*((1-t)*P0+tP1)+t((1-t)P1+tP2 )

=（1-t)² *P0+2t*(1-t)*P1+t²*P2  ;t[0,1];

代码：

    public LineRenderer line_b;     public LineRenderer line_a;     public LineRenderer line_c;      public Transform start;     public Transform end;     public Transform c;      void Start()     {           }     void Update()     {          line_a.SetPosition(0, start.position);         line_a.SetPosition(1, c.position);         line_c.SetPosition(0, end.position);         line_c.SetPosition(1, c.position);             // float distance = Vector3.Distance(start.position, end.position);         Vector3 controlPoint = c.position;             //start.position + (start.position+ c.position).normalized * distance / 1.6f;          Vector3[] bcList = GetBeizerPathPointList(start.position, controlPoint, end.position, 50);         line_b.positionCount = bcList.Length + 1;         line_b.SetPosition(0, start.position);         for (int i = 0; i < bcList.Length; i++)         {             Vector3 v = bcList[i];             line_b.SetPosition(i + 1, v);         }       }     public static Vector3[] GetBeizerPathPointList(Vector3 startPoint, Vector3 controlPoint, Vector3 endPoint, int pointNum)     {         Vector3[] BeizerPathPointList = new Vector3[pointNum];         for (int i = 1; i <= pointNum; i++)         {             float t = i / (float)pointNum;             Vector3 point = GetBeizerPathPoint(t, startPoint,                 controlPoint, endPoint);             BeizerPathPointList[i - 1] = point;         }         return BeizerPathPointList;     }      //贝塞尔曲线二次方公式     private static Vector3 GetBeizerPathPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2)     {         return (1 - t) * (1 - t) * p0 + 2 * t * (1 - t) * p1 + t * t * p2;     }

三阶贝塞尔曲线

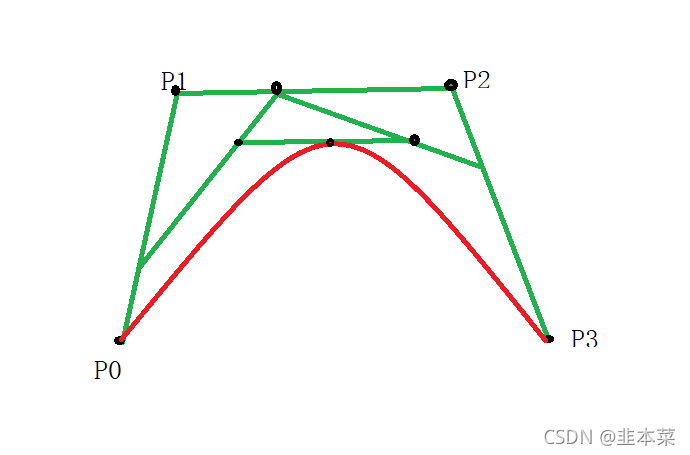
三阶贝塞尔曲线和二阶其实是同一个道理，都可以按照一阶的贝塞尔方程来进行线性插值。这里就直接上公式了。

P(t)=P0*(1-t)³ +3P1*t*(1-t)²+3P2*t²*(1-t)+P3*t³ ; t[0,1]; 

代码

 public Transform start;     public Transform end;     public Transform c0;     public Transform c1;      public LineRenderer line_b;     public LineRenderer line_a;     public LineRenderer line_c;     public LineRenderer line_d;     void Start()     {              }      // Update is called once per frame     void Update()     {         line_a.SetPosition(0, start.position);         line_a.SetPosition(1, c0.position);          line_c.SetPosition(0, c1.position);         line_c.SetPosition(1, c0.position);          line_d.SetPosition(0, c1.position);         line_d.SetPosition(1, end.position);            Vector3[] bcList = GetBeizerPathPointList(start.position, c0.position,c1.position, end.position, 50);         line_b.positionCount = bcList.Length + 1;         line_b.SetPosition(0, start.position);         for (int i = 0; i < bcList.Length; i++)         {             Vector3 v = bcList[i];             line_b.SetPosition(i + 1, v);         }      }      public static Vector3[] GetBeizerPathPointList(Vector3 startPoint, Vector3 controlPoint0, Vector3 controlPoint1, Vector3 endPoint, int pointNum)     {         Vector3[] BeizerPathPointList = new Vector3[pointNum];         for (int i = 1; i <= pointNum; i++)         {             float t = i / (float)pointNum;             Vector3 point = GetBeizerPathPoint(t, startPoint,                 controlPoint0, controlPoint1, endPoint);             BeizerPathPointList[i - 1] = point;         }         return BeizerPathPointList;     }        //贝塞尔曲线三次方公式     private static Vector3 GetBeizerPathPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2,Vector3 p3)     {         return (1 - t) * (1 - t) * (1 - t) * p0 +                 3 * p1 * t * (1 - t) * (1 - t) +                 3 * p2 * t * t * (1 - t) +                 p3 * t * t * t;     }